If you’re simply looking to buy shares or invest in an index fund – CFDs won’t be for you. But, if you’re looking to deploy more advanced trading strategies – such as applying leverage or short-selling, then CFDs might be the solution.
Put simply, CFDs are tasked with tracking the value of an asset like-for-like. This means you won’t own the CFD instrument, but you can still profit from ever-changing price movements.
In this guide, I am going to discuss everything there is to know about CFDs. I’ll cover how CFDs work, what you can trade, how leverage and short-selling can be accessed, and what sort of cost-savings this financial instrument offers. I’ll also talk about my favorite CFD trading platform: eToro.
What are CFDs?
CFDs are contracts-for-differences. They are financial instruments created by online brokers and trading platforms. The primary goal of a CFD is to track the real-world price of an asset. For example, if Tesla stocks move from $400 to $400.50, the CFD instrument will mirror this.
Similarly, if the market price of Gold goes down by 2.2%, as will the CFD. The most important thing to understand about this complex financial instrument is that by trading it, you won’t own the underlying asset. For example, if you place a $500 buy order on Bitcoin CFDs, you won’t own $500 worth of Bitcoin.

On the contrary, this is the amount that you are staking on the position. In turn, if Bitcoin increased by 10% in value, your $500 stake would now be worth $550. Although at first glance you might be put off by the fact that you won’t own the asset you are trading, CFDs come with several perks.
As I explain in more detail shortly, this includes:
- Low or even zero commissions on most CFD trading sites
- Ability to apply leverage – meaning you can trade with more than you have in your account
- CFDs allow you to short-sell assets, so you can profit from falling markets
- Spreads are usually very tight when trading CFDs – further reducing your costs
- Allow you to access difficult-to-reach markets, such as crude oil, natural gas, or stocks listed in the emerging markets
All in all, CFDs offer traders an alternative to traditional asset classes like stocks, mutual funds, or ETFs.
How do CFDs Work?
As noted above, CFDs are created by your chosen broker. The objective of each CFD instrument is to monitor real-world asset prices in real-time. What goes up in the traditional financial markets will also go up on your CFD trade – and vice versa for falling prices.
Let’s look at a quick example of how a CFD trade might pan out:
- You are interested in trading crude oil – which is currently priced at $41.20 per barrel
- You have no interest in taking delivery of physical barrels of oil, nor do you have the financial means to purchase futures contracts
- As such, you opt for crude oil CFDs
- You think that at $41.20 per barrel, oil is heavily underpriced
- With this in mind, you place a ‘buy order’ worth $1,000
- A few days later, crude oil is priced at $44.90 – meaning it has increased by 9%
At this point in the trade, you might be tempted to cash in your profits. In order to do this, you would need to place a ‘sell order’. In doing so, you made 9% on a stake of $1,000 – translating into gains of $90 less fees. If you were to go short on this trade, you would have needed to place a ‘sell order’. Then, to close the position, a ‘buy order’ would need to be placed.
What CFDs Assets can you Trade Online?
One of the most appealing things about CFDs is that you can invest in virtually every asset class and financial market imaginable. Once again, this is because the asset itself does not exist. Instead, the instrument is only tracking the asset’s real-time price.
Below I have listed some of the many CFD markets that you will have access to when trading online:
- Stocks: You can speculate on the future value of stocks and shares. This includes major markets like the NASDAQ and NYSE, as well as exchanges based in Europe, Australia, Japan, Canada, and more.
- Forex: You can trade dozens of currency pairs via CFDs.
- Indices: Stock market indices like the NASDAQ 100 and FTSE 100 can be traded via CFDs with ease.
- Hard Metals: Trading gold, silver, copper, and other hard metals can be done via most CFD brokers.
- Energies: Oil and natural gas are popular with CFD traders.
- Cryptocurrencies: I would argue that trading cryptocurrencies via CFDs is a lot safer, convenient, and cost-effective than using a trading exchange. More on this later.
It is important to remember that not all trading sites will offer the above CFD markets. As such, you’ll need to check this out before opening a trading account.
Benefits of CFDs
I mentioned earlier that CFDs come with several perks that you won’t find with traditional asset classes. I elaborate on these benefits in more detail below.
Short-Selling
By using a traditional stockbroker and subsequently buying shares. there is only one thing that you can hope for. That is to say, you will only make money if the value of the shares goes up.
But, what do you do if you think that the markets are overinflated or that a specific stock is likely to drop in price? Well, you’d likely be forced to cash out your investment and wait for the markets to once again move in an upward direction.
The good news is that CFD platforms allow you to profit from your bearish hypothesis through the art of ‘short-selling’.
In its most basic form, this means that you can speculate on the price of an asset going down. If the asset in question does drop in price, you will make a profit. And of course – if the opposite happens and the asset goes up in value, you will make a loss.
If you’ve never engaged in short-selling before, here’s a quick example of how that would work when trading CFDs:
- You think that at $15,500 – the price of Bitcoin is overvalued and thus – a downtrend trend is likely
- You place a sell order with your chosen CFD broker
- You decide to stake $500 on the trade
- A few days later, Bitcoin has dropped back down to $11,800
- This represents a rapid decline of 23%
- This is great news for you as you went short via a sell order
- You decide to cash in your profits by placing a buy order
Now, on a stake of $500, you made a total profit of $115. This is because Bitcoin dropped by 23% – so you simply need to multiply this figure by $500.
Leverage
An additional benefit of trading CFDs is that you will almost always be offered leverage by your chosen platform. As I briefly mentioned earlier, this means that you can trade with more money than you have deposited in your CFD broker account.
Leverage is usually expressed as a ratio – such as 1:2, 1:10, or 1:30. This represented the multiplier that you will get on your position. For example, if you stake $100 with leverage of 1:10, your trade is worth $1,000. Similarly, if you stake $300 and apply leverage of 1:2, your trade is worth $600.
I’ll get to the specifics of liquidation and limits shortly, but first, let me give you an example of how a leverage CFD trade would work in practice.
- You want to trade gold – which is current priced at $1,950 per oz
- You think that gold is due to go on an upward trajectory as per the market uncertainties of COV-19 and the US election
- As such, you place a $500 buy order
- Only this time, you apply leverage of 1:20
- This means that in theory, you are trading with 20 times your stake of $500 – which is $10,000
- Fast forward a few weeks and gold is now trading at $2,300 per oz
- This represents an increase of 17%
Under normal trading conditions, gains of 17% on a $500 stake would have made you a profit of $85. However, you were trading with leverage of 1:20. This means that your gains of $85 are amplified by a factor of 20 – taking your all-in profits to $1,700.
If you think that leverage sounds a bit too good to be true – it kind of is. This is because you face the risk of being ‘liquidated’ if your prediction does not come to fruition. This is where the broker closes your trade automatically when the trade goes in the red by a certain amount.
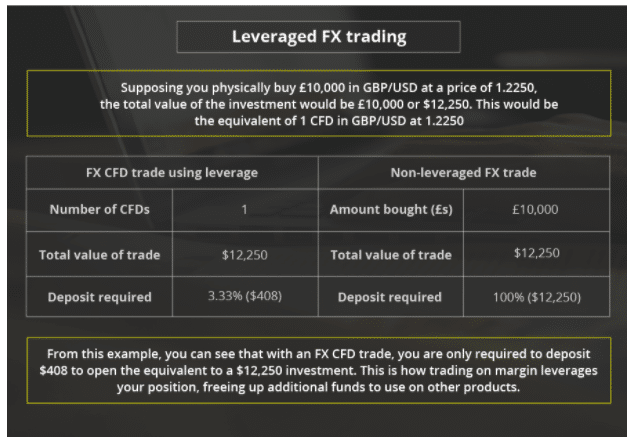
In the example I gave above, applying leverage of 1:20 meant that a $500 stake was increased to $10,000. This means that you have a ‘margin’ of 5% ($500 of $10,000). As such, if the price of gold declined by 5%, your broker would close the trade and you would lose your $500 margin.
In other words, while trading CFDs with leverage can be great when you are making gains, it can very quickly lead to large losses.
Lower Commissions and Spreads
As the underlying asset backing a CFD instrument does not exist, the trading fees applicable are going to be much lower. In fact, there are several trading platforms out there – such as eToro, that offer ridiculously low fees on CFD markets.
Difficult-to-Access Markets
As I mentioned earlier, CFDs allow you to trade virtually any asset class going. Whether that’s cryptocurrencies, forex, stocks – CFD brokers have you covered. But, I should dig a little deeper here by saying that CFD platforms go above and beyond when it comes to difficult-to-access markets.
** below content does not apply to US users
For example, if you were trading stock CFDs at eToro, you would be able to enter buy and sell positions on 17 stock exchange markets. This covers everything from the UK and the US to Saudi Arabia and Hong Kong. This also rings true for the likes of wheat, corn, silver, gold, and copper.
Ultimately, CFD trading platforms are not confined in the number of markets they offer or the types of assets you can access. This allows you to diversify into areas of the financial markets that traditional brokers typically steer clear of.
Drawbacks of CFDs
CFDs also come with several drawbacks that might make them unsuitable for your personal financial goals.
This includes the following:
No Ownership of the Asset
As I have noted several times already, by trading CFDs you do not own the asset in question. For example, if you trade gold CFDs you have no legal right to the hard metal. Similarly, if you trade Apple stock CFDs, you do not own Apple shares.
In my opinion, this is more of a personal preference than an all-out drawback. By this, I mean that if your primary trading goal is to make consistent profits – then it doesn’t really matter whether or not you own the asset.
After all, the end game is the same – if you speculate the future price of the asset correctly, you make money. If you don’t, you lose money.
Dividends When Trading CFDs
When you buy a stock in the traditional sense – you are entitled to dividends as and when they are paid. Your share is determined by the number of shares you hold. In the case of stock CFDs, you don’t own the asset, and thus – you have no legal right to dividends. With that said, some CFD platforms do actually allow you to earn dividends – well, sort of.
The way it works is as follows:
- Let’s suppose that you are interested in trading Nike stock CFDs – which are priced at $127
- You place a buy order worth $1,270 – so you are effective trading 10 Nike stocks
- Nike distributes a dividend payment of $1.27 per share
- As you are long on Nike, the CFD broker will credit your trading account with $12.70 (10 x $1.27)
Now, I should clarify that this dividend payment is not covered by the respective company itself – in this case, Nike. On the contrary, those going short on Nike stock CFDs via sell orders will have a negative payment debited from their trading account.
That is to say, somebody shorting 10 Nike stocks would have $12.70 dedicated from their balance at the respective trading platform.
No US Citizens
If you’re based in the US and looking to trade CFDs – you’re out of luck. This is because both the Commodity Futures Trading Commission (CFTC) and the Securities and Exchange Commission (SEC) do not permit US citizens to open CFD trading accounts.

This is the case with brokers based in and out of the US. This is why popular platforms like eToro do not accept US traders. While there are several ‘offshore’ CFD platforms allowing anyone to open an account – including US clients, these are usually unlicensed, and thus- you should avoid them.
Most CFD Traders Lose Money
When you visit your chosen CFD trading platform – you will, as per regulatory demands, be presented with a disclaimer at the top/bottom of the page. This outlines the number of traders that lose money at the respective platform – in percentage terms. This is often between 71% and 85%.
One of the main reasons for this is that newbie traders do not respect the risks of leverage. As I covered earlier, while leverage allows you to amplify your potential profits, it also does the same for losing trades. This is why you must ensure that you have sensible risk-management tools in place – which I cover shortly.
How to Place a CFD Trade
Although CFD instruments are complex financial instruments, the process of actually placing a trade doesn’t need to be difficult. With that said, some platforms are more user-friendly than others, which is why a lot of newbies opt for eToro.
Nevertheless, there are several order types that you need to understand before you take the CFD trading plunge, which I outline below.
Buy and Sell Positions
Irrespective of what trade you are planning to deploy, all positions must be entered with either a buy or sell order. Put simply, this lets the broker know whether you think the asset will rise or fall in value.
A buy order illustrates that you think the asset will rise, and a sell order illustrates that you think it will fall.
As I covered earlier, if you enter the trade with a buy order, then you will need to place a sell order to close it. This works the same when entering a position with a sell order but in reverse.
Entry Price
Whether you’re looking to trade stocks, energies, hard metals, cryptocurrencies, or any asset for that matter – CFD prices change on a second by second basis. As such, you need to let your chosen CFD trading platform know how you wish to enter the market. In this sense, you have two options – a limit order or a market order.
A market order is the basic option to take. This will see your chosen broker execute your buy or sell order instantly. It will do so at the next available market price. This means that your entry price will be slightly above or below the price you see on-screen.
For example:
- You are interested in placing a buy order on Tesla stock CFDs
- Tesla is currently priced at $410.50
- You don’t want to miss the opportunity to enter the market so you place a buy order
- Your buy order is executed a couple of seconds later at a price of $410.54
Equally, your entry price on the above Tesla stock CFD buy order could have been just below the initial price of $410.50.
On the other hand, most CFD traders in the online space will opt for a limit order when entering a new position. Unlike a market order, this allows you to specify the exact price that your trade is executed at. This allows you to deploy a more systematic entry and exit strategy on your trade.
For example:
- You are interested in placing a buy order on Tesla stock CFDs – which are currently priced at $410.50
- Although you are bullish on Tesla, you want to enter the market when the shares next take a temporary dip
- As such, you enter a buy limit order at $389.98
- This is 5% below the current stock price of Tesla
- A few days later, Tesla shares take a dip and subsequently fall below $389.98
- As such, your buy limit order is matched by markets and is now live
As per the above, your limit order allowed you to enter your Tesla stock CFD trader at a more favorable price. In this case, that’s a 5% discount. In theory, if and when the stock price of Tesla recovers back to $410.50, your potential gains are already 5% higher than they would have been had you opted for a market order.
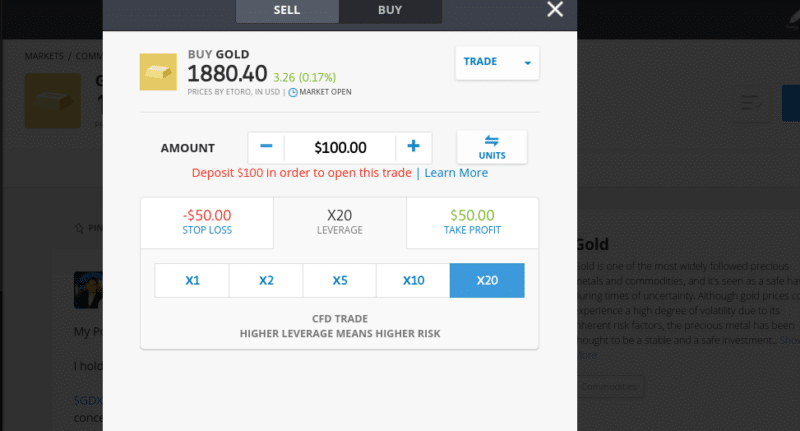
Leverage Ratio
If you are planning to apply leverage to your CFD trade, you need to specify this before you place your order. Before I get to that, it is important to note that you will be restricted in how much leverage you can apply.
The limits are based on:
- The CFD trading platform itself
- Your country of residence
- The asset you are trading
- Whether you are a retail client or professional trader
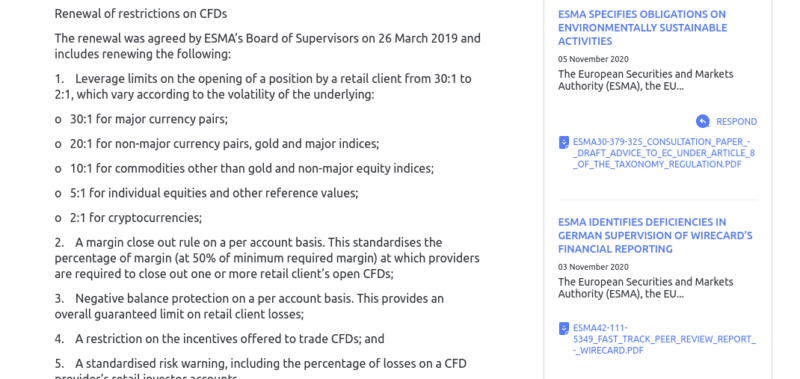
So, if you’re based in the UK or Europe – your leverage limits are dictated by the European Securities and Markets Authority (ESMA).
ESMA limits are as follows:
- 1:30 on major forex pairs
- 1:20 on minor/exotic forex pairs, gold, and major indices (e.g. S&P 500)
- 1:10 on commodities other than gold (e.g. oil) and non-major indices (e.g Germany 30)
- 1:5 on stocks
- 1:2 on cryptocurrencies
The limits listed above were installed by ESMA to protect retail clients from risking more than they can afford to lose. In other regions, Australian traders are not restricted in how much leverage they can apply at the time of writing.
However, in April 2021 Australians will be restricted by the same ESMA limits discussed above. Other parts of the world can and will have different rules on how much leverage you can apply.
With that being said, you can get significantly higher limits if you are deemed to be a professional trader. In order to meet the threshold outlined by ESMA (and several other regulatory bodies), you need to meet two of the following three criteria:
- Have previously worked in the financial services industry and have suitable experience with leveraged instruments
- Have an investment portfolio of €500k or more
- Prior trading experience consists of at least 10 positions every three months for a reasonable amount of time
Taking all of the above into account, when it comes to selecting your leverage ratio while filling out your CFD trading order form, your limits will be shown on-screen. If, for example, you want to trade stocks at leverage of 1:5, you simply need to select the ‘5x’ button.
Stop-Loss
All CFD trading platforms give you the ‘option’ of setting up a stop-loss order in addition to your buy/sell and limit/market orders.
Although not compulsory, I would strongly suggest that you make use of stop-loss orders as this is the most important risk management tool that you have at your disposal. For those unaware, a stop-loss order allows you to instruct your broker to close your position if it goes into negative territory by a specified amount.
For example, you might be looking to speculate on the value of oil going down, but you don’t want to lose more than 10%. As such, you’d need to set up a stop-loss order at a price of 10% above your buy/sell price.
Here’s a practical example of how to set up a stop-loss order, and why they are crucial when trading CFDs:
- You are interested in trading the Dow Jones Index, which is currently priced at 29,420 points
- You think the value of the index will rise, so you place a buy order
- You don’t want to lose more than 5% of your stake, so you also set up a stop-loss order
- You set the stop-loss order at 27,949 points
- The Dow Jones Index begins to take a turn for the worse and is now priced 10% lower
- However, your buy order was automatically closed when the price hit 27,949 points, meaning that you reduced your losses to just 5%
As you can see from the above, it doesn’t matter how much further the Dow Jones Index decline goes, as your trade was closed at the 5% mark. This is why stop-loss orders are such an important and effective way to mitigate your CFD trading risks.
Take-Profit
Much like stop-loss orders, take-profit orders are not compulsory. However, I would once again advise you to consider placing take-profit orders on each and every CFD trade that you deploy.
In doing so, you will be instructing your broker to close your buy or sell position when it hits a specified profit target. In other words, this works in the same way as a stop-loss order but in reverse.
Here’s an example of how a take-profit order works in practice:
- Sticking with the same example as above, you have placed a buy order on the Dow Jones Index at 29,420 points
- You have already set up your stop-loss order at 5% below this price
- You want to make 12% in gains on this trade, so you place a take-profit order
- You set your take-profit order at a price of 32,950 points, which is 12% above the current price
As per the above example, you have now set up a CFD trade that can only result in one of the two outcomes. If the trade goes to plan, then your take-profit order will be activated when the Dow Jones Index increases by 12%. But, if things don’t go to plan and the Dow Jones Index drops by 5%, your stop-loss will be activated.
Crucially, by placing both of the above orders, you don’t need to sit at your computer and wait for the trade to unfold. If anything, this is a super-inefficient way of trading. Instead, the trade will close organically when the take-profit or stop-loss order is matched by the markets.
CFD Trading Fees
It is also important that you have a firm idea of how CFD trading fees work. This is because the likes of commission, spread, and overnight financing can and will have a direct impact on how much profit you will retain.
Here’s what you need to know:
Commissions
Some CFD trading sites in the online space will charge a variable commission. This is charged every time you place a buy and sell position. For example, the broker might charge 0.2% per slide – meaning you’ll pay 0.2% of the amount you initial stake, and 0.2% of the amount you sell your position at.
Here’s a practical example:
- You want to place a buy order worth $400 on Bitcoin CFDs
- Broker charges a commission of 0.5% on cryptocurrencies, so this costs you just $2
- When you sell your Bitcoin CFD position, it is worth $600
- Once again, you pay 0.5% – amounting to a commission of $3
Spreads
Spreads are something that you will find at all online brokers and trading platforms. It is the difference between the buy price and sell price of your chosen asset. The difference can be viewed in ‘pips’, but I find it much easier to calculate it in percentage terms.
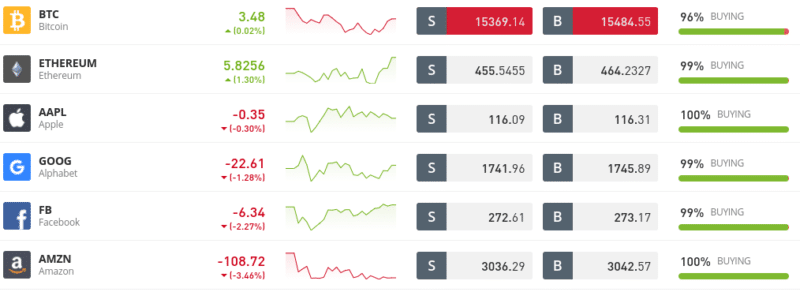
For example, let’s look at what the spread amounts to when trading Facebook stock CFDs at eToro:
- To go long on Facebook stock CFDs, you will pay a buy price of $273.17
- To go short on Facebook stock CFDs, you will pay a sell price of $272.61
- The difference between the two prices is 0.20% – which is typical for stock CFDs at eToro
So what does this mean in real terms? Well, irrespective of whether you go long or short on Facebook, as soon as the order is placed you will immediately be -0.20% in the red.
For example, if the value of your position is $200, your trade will be worth $199.60 – representing a small loss of $0.40. As such, you would need to see your buy or sell position grow by at least 0.2% to get back to the ‘break-even point’.
For example, when buying stocks through a traditional broker, you will most certainly pay more than this. There is the odd exception to this rule – such as Robinhood and of course – eToro.
Overnight Financing
Make no mistake about it – overnight financing is one of, if not the most important fee that you need to factor into your CFD trading costs. Put simply, all CFD instruments are leveraged financial products. As such, you will be charged an interest fee for every day that you keep your position open.
This is known as ‘overnight financing’ or in some cases – ‘swap fees’. Either way, this is a trading fee that you will always pay on your CFD position if you keep it open for more than one day. The specific time of the day that the charge kicks in will vary from broker to broker and asset to asset.
Note: Overnight financing fees still come into play even if you do not apply any leverage on your CFD trade.
Nevertheless, this is why CFD trading is largely suited to short-term strategies. But, this isn’t to say that you can’t keep a CFD position open for longer and still make a profit. On the contrary, the fact of the matter is that as long as your gains outweigh the amount you paid in overnight finance, profits can still be had.
Now, the amount that you pay is based on an annual interest charge that will vary depending on the market. This can make it super-confusing to know exactly what you are being charged and thus – how much you need to make to cover the cost.
With that said, I like the fact that eToro displays the overnight financing charge in dollars and cents. This is displayed as a Monday-to-Friday rate and also a weekend rate. This is because some CFD overnight financing fees come at a premium when held on Saturday and Sunday.
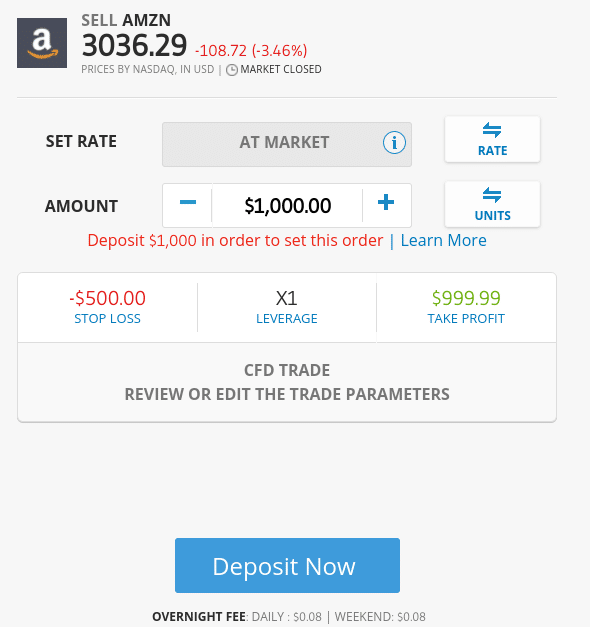
To give you an idea of what sort of overnight financing fees you might incur when trading CFDs, I have collated a couple of examples from eToro:
- If I was to buy Amazon stocks at eToro without applying leverage, this would be classed as a traditional share purchase. As a result, no overnight financing fees would come into play
- But, as soon as I change this to a short-selling order, this translates the position into a CFD trade
- As per the screenshot above, I am being quoted a price of $0.08 per day on a stake of $1,000 – with no surcharge over the weekend
- If I were to keep this short-selling order open for a full year, it would cost me $29.20 in overnight financing fees on a stake of $1,000
- In percentage terms, this amounts to an annual overnight financing rate of just 2.92%.
This actually offers great value when you think about it. After all, if you were looking to short-sell a stock for a whole year, you would be looking to make more than 2.92% in gains.
Now let’s look at a slightly more elaborate example that includes leverage.
- In this example, let’s suppose that you are super-bullish on the US stocks markets
- As such, you decide to go long on the S&P 500 Index
- You decide to risk $1,000 and apply leverage of 1:5. In effect, this means that you are staking a total of $5,000 on the S&P Index increasing in value
- As per the screenshot below, you will pay an overnight financing fee of $0.41 per day and $1.22 to keep the position open over the weekend ($3.27 per week)
- This means that were you to keep your 5x leveraged S&P 500 CFD trade open for one year, you would pay a total of $170.04 in overnight financing
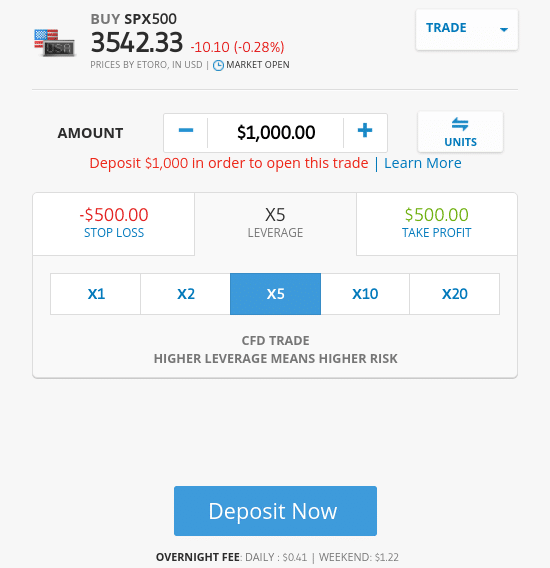
As per the above – and based on a total position value of $5,000 – you are paying 3.4% per year. Once again, this does offer good value – especially considering you are trading with leverage of 1:5. If, for example, you were to short-sell the S&P 500 during a financial crisis, the potential gains could be highly lucrative.
CFD Risk Management
As I noted earlier, the vast majority of CFD traders lose money. While this is usually through a lack of respect for leverage, ultimately – major losses are incurred because there is no risk management plan in place.
With this in mind, below I have listed some useful risk management strategies that you might want to consider when starting your CFD trading journey.
Entry and Exit Plan
Going into a CFD trade without a plan of action is asking for trouble. Instead, you should set yourself some clear goals. In order to do this, you simply need to ensure that each and every trade that you place comes with a stop-loss and take-profit order.
In terms of price targets and maximum loss, this depends on your personal CFD trading strategy. For example, if you are looking to day trade CFDs, then you might take a risk/reward ratio of 1:4. This means that for every $1 that you risk, you stand to make $4 in gains. In other words, you only need one successful trade out of every five to break even.
If you’re looking to take a slightly longer-term approach to trading, then your take-profit target is likely to be much bigger.
Bankroll Management
All seasoned CFD traders that make consistent gains do so because they respect the principle of ‘bankroll management’. In simple terms, this refers to the maximum amount that you should stake on a single trade. By not breaching this threshold, you will give yourself the best chance possible of depleting your trading capital.
This should be viewed in percentage terms. In doing so, your stakes will increase over time as your trading capital grows. For example, you might decide to limit your maximum trade size to 1% of your account balance. As such, a $4,000 balance would not allow you to stake more than $40 on each trade.
If, for example, you were able to grow your capital to $6,000 by the end of month 3, then your maximum stake would now stand at $60 per trade. Similarly, if your account balance went in the wrong direction and was now worth just $3,000, the maximum stake would be reduced to $30.
Why you Might Consider Trading Cryptocurrencies via CFDs
Before I conclude my guide on CFD Trading, I wanted to dedicate a quick section to cryptocurrencies. The reason for this is that if you are a keen cryptocurrency trader, or you are planning to access this particular marketplace, CFDs are a far better facilitator for this purpose.
For example, if you are using a conventional cryptocurrency exchange to trade, there is every chance that the platform is not regulated by a reputable body. In addition to this, most cryptocurrency exchanges do not accept fiat currency deposits. 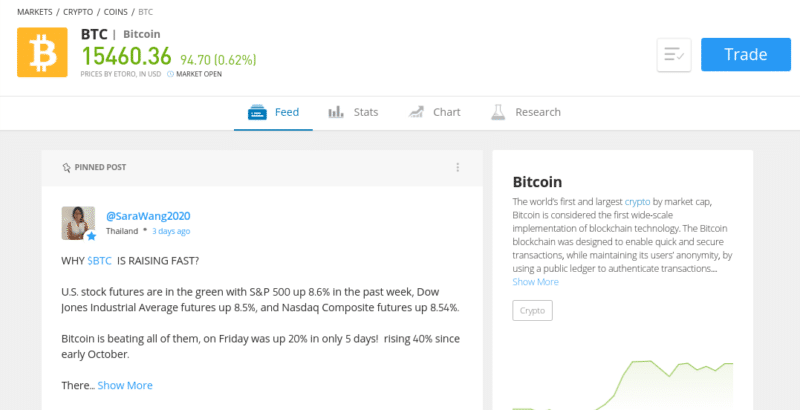
This means that you will need to fund your account with a cryptocurrency. This is also the case with withdrawals. In addition to this, most cryptocurrency exchanges do not allow you to trade digital currencies against a fiat currency. For example, instead of trading BTC/USD, you will likely be trading BTC/USDT.
At the other end of the spectrum, CFD trading sites must be regulated. For example, eToro is licensed by the FCA (UK), ASIC (Australia), and CySEC (Cyprus). In turn, this means that you can rest assured that your money is safe, not least because the aforementioned licensing bodies require brokers to keep client funds in segregated bank accounts.
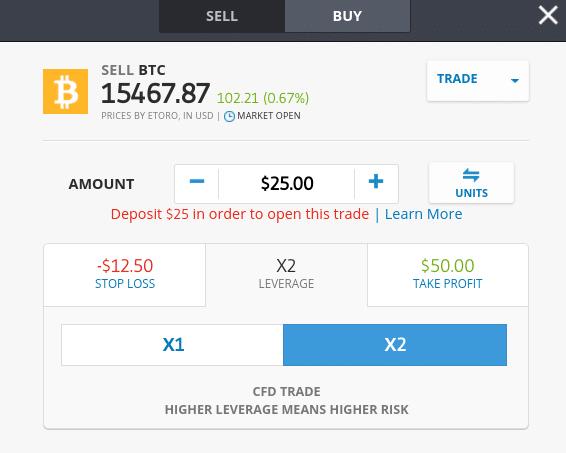
You will also have the added benefit of being able to short-sell a cryptocurrency and even apply leverage. By using a CFD broker to trade cryptocurrencies, you will also be able to easily deposit and withdraw funds.
eToro accept debit/credit cards and bank transfers. The former also supports e-wallets like Paypal, Skrill, and Neteller. Ultimately, if you are looking to trade cryptocurrencies in a safe, convenient, and low-cost manner – while at the same time benefit from short-selling and leverage facilities, you might want to consider CFDs.
CFD Trading: The Bottom Line
In summary, CFD trading won’t be for everyone. For example, if you are more of a passive, long-term investor that likes to take a ‘buy and hold’ strategy, then you are best off using a traditional broker. Similarly, if you don’t have the time to actively trade or you have the required knowledge to succeed, CFDs might not be your calling.
76% of retail investor accounts lose money when trading CFDs with this provider. You should consider whether you can afford to take the high risk of losing your money.
But, if you are looking to trade financial assets in a low-cost environment and heavily regulated ecosystem, the CFD arena is likely going to be your best option. For example, in addition to being able to trade assets in a cost-effective manner, you will have access to thousands of markets.
This includes everything from stocks and bonds to gold and natural gas. Plus, all CFD markets can be short-sold, subsequently allowing you to profit from falling markets. If you want to increase your risk/reward ratio, CFDs can also be traded with leverage.
As always, there is every chance that you will lose money when trading CFDs. In fact, most people make a loss at the first attempt of trying, so do bear this in mind.


Leave a Reply